SQUARING BERKLEY LANE
The crop circle at Berkley Lane appeared June 10th 2012.
At first sight it was not a spectacular one: no Mayan symbolism, no esotheric-, subconscious- or alien message to find.
I have always loved the 'simple' circles. Often there was something about it that was not simple at all and I suspected with this one the same.
Men like John Martineau, Alan Brown, Michael Glickman, Nick Kollerstrom and Bert Janssen have done a lot of research about -sacred- geometry and a recurring theme is often the squaring of the circle.
It goes beyond the purpose of this article to explain everything about this topic but on the internet you can find a lot of information.
In Michael Glickman's article Why-pi? on his website (http://www.michaelglickmanoncropcircles.com/blog/why-pi/) he asked for help:
"It only remains to find that Frome squares the circle. I cannot do it. I have asked Allan Brown to help. Anyone out there?"
I expected a lot of reactions to his call but everything kept silent. Although I never did this before but what if I tried to find the solution?
So I printed the image, pulled out my compass and ruler, started measuring and drawing and found -much quicker than I thought- the solution to his question......ehhh sorry......THREE solutions to his question.
After checking and re-checking I have e-mailed Michael a few days later and asked if he wanted my files to see if I was right and if so that he was free to use them to publish. After a reminder to him a week later I finally got an e-mail that it was okay to send my solution, so I did.
This is the e-mail I sent to him:
July 12, 2012 at 2:38 pm
Hi Michael,Thanks for another one of your fine articles.
I am happy to let you know that I am ‘the one out there’ because I succeeded in squaring this circle.
I will send the file as soon as possible and if you want you can use it on your website,
Kind regards,
I have never heard from Michael since..........very strange.
Was I right or was I wrong? He didn't even send me an email to tell me what was the matter.
I highly respect all his work and amazing discoveries on the geometric characteristics of crop circles and but I was very disappoin-ted in the way he simply ignored my contribution for reasons I don't know.
I think it has nothing to do with me personally because a reaction to Michael Glickman a few months later probably was not answered as well.
This message was sent September 5 and was followed by an other one a day later (for privacy reasons I only put the initials of the writer of the message):
Hello Michael.I enjoy reading this blog. You write in a delightful way.I have a thought concerning the squaring of the Frome circle: Two of the tram lines (the two right ones from the perspective of the photo used here) touch the sides of two of the circles. Actually, both of them touch the inside of a ring. If you connect the points where these two tram lines cross the perimeter of the big circle, you get some kind of four-sided geometrical figure with the same perimeter as a square that would fit neatly into the big circle. (I have measured the diameter of the circle parallel with the tram lines to get to this conclusion, but since I only have used the photo in this blog, and no ground measurements, it might be that I am wrong…).Maybe that’s a strange way of squaring the circle, but it intrigued me. As far as I can understand, this would not have happened, had the crop circle been just a bit larger or smaller. P. N. September 5, 2012 at 10:52 pm
I see now that I have misunderstood the meaning of “squaring the circle”. I took it to mean fitting a square either precisely outside the circle or precisely inside the circle, but I have now seen that it is about finding a square with the same area as the circle. Sorry about that.However that rightmost tramline that touches the circle centered in the middle, seems to me to pass through the crop circle exactly the same length as the side of a square with the same area as the circle. Maybe that would be squaring the circle? P. N. September 6, 2012 at 10:14 pm

P.N. comes very close to the solution as you will see in the following article, earlier published on the Cropcircleconnector in august or september 2012. After re-reading this article again I think I jumped to conclusions to quickly so I have re-edited it and added extra images to make everything more clear.

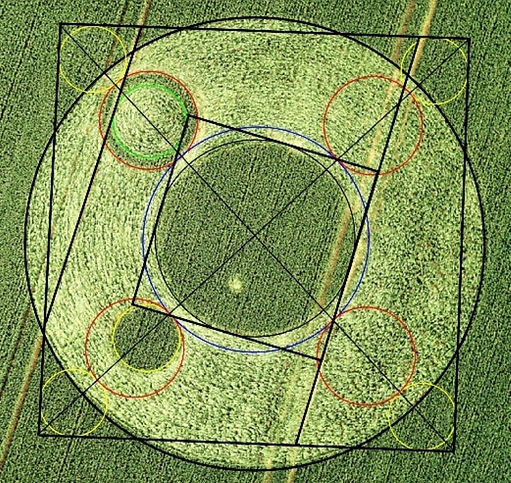
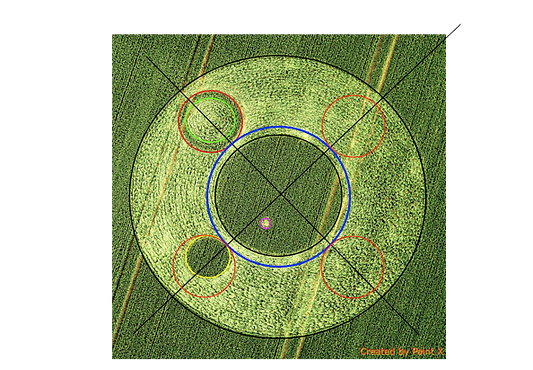
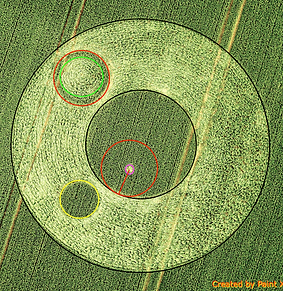
In the right image I have highlighted and numbered the circles which all play a role in the squaring and I will take steps to lead you to the final conclusion.
Squaring Berkley Lane
Circle 1=big outer circle (black)
Circle 2=center circle standing crop (black)
Circle 3=outer perimeter of circle with standing ring (red)
Circle 4=small circle standing crop (yellow)
Circle 5=very small circle in circle 2
Circle 6=virtual circle with midpoint of circle 2 and touching circles 3 and 4 (blue)
Circle 7=inner perimeter of the standing ring of circle 3 (green)
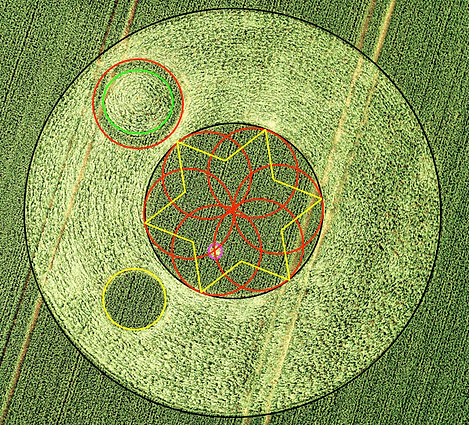
1) SQUARING THE MAIN CIRCLE
Draw the center axis through circle 2 and 3 and extend it outside circle 1
Do the same with circle 2 and 4
Draw a circle around circle 2 which touches circles 2 and 3 ( circle 6)
Copy outer perimeter of circle 3 three times to the other axes so, that they are centered and that their perimeter touches circle 6
Copy circle 4 four times and put it 'on top' of the circles of step 4 and center it on the axes
Draw a square around the circles of step 5: this is the square that defines the squaring of the main circle (shown
in green).
2) INTERLUDE
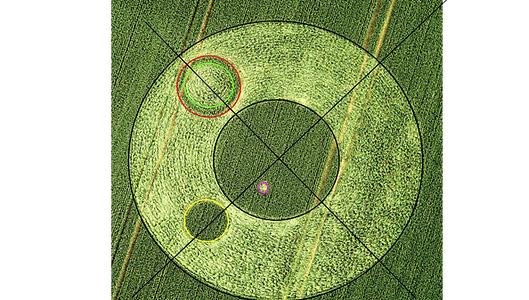
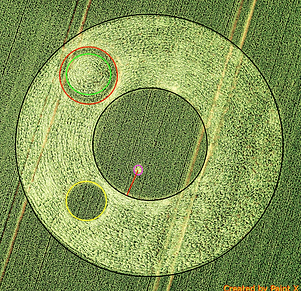
And what about the the very little circle in the center circle (circle 5)?
Why is it there? What does it say?
It appears that the distance of the center of it to the edge of circle 2 is the radius of circle 3.
Circle 3, copied six times in circle 2, fits great, forming a flower pattern.
I am also intrigued by the circle formed by the inner perimeter of circle 3 (the one with the standing ring) which i will call circle 7.
I wonder if it does have a function in the total design but now i do not see it.
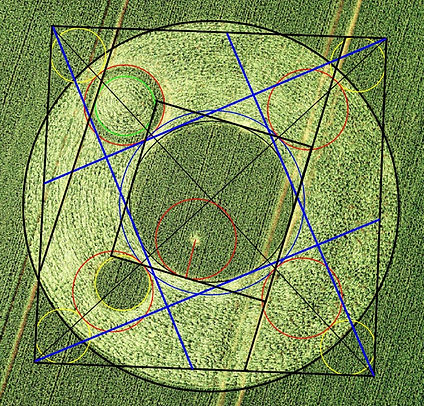
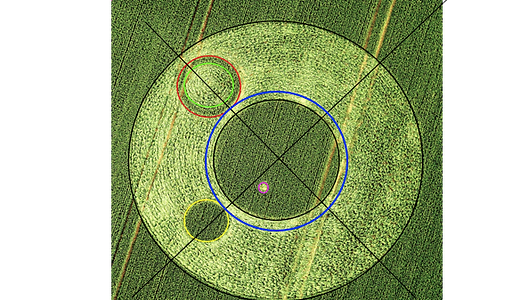
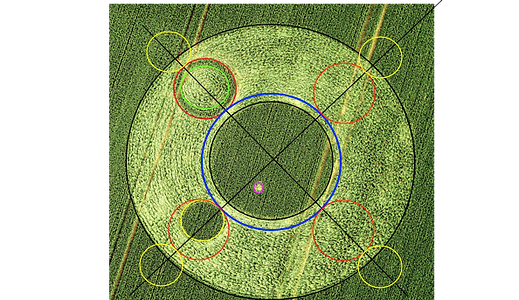
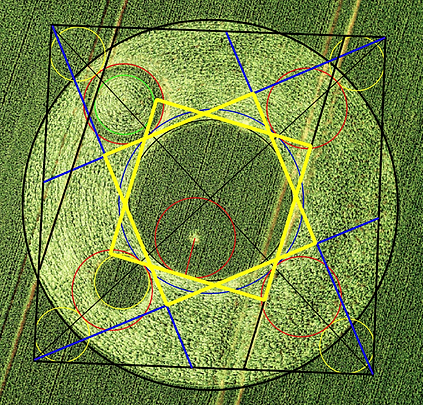
3) SQUARING A VIRTUAL CIRCLE
This was what I found a day later..........
Update July 13
After having yesterday's result I could not stop thinking about this crop circle and everytime I went back to it, stared at it and tried to find more but i did not know exactly what, until.......
Circle 6, which touches circles 3 and 4, does not actually exist in the field but on paper it does and it appears to be an important part of the design.
So would it not be nice to see if it is possible to square this one as well?
And again i found the solution!
Draw four lines, each starting in the corners of the 'big square' and running tangent to circle 2.
The result is squaring the -virtual- circle 6!!
As well as circle 6, the corner points do not exist in the field but they too form an important part of the design.
4) IT DOES NOT LET ME GO
Update July 14 2012
I can't keep my thoughts from this crop circle so this morning i made some prints and again stared at them for some time.
Suddenly i see something i have totally overlooked in first instance.
How could i be so shortsighted?
The tramlines!!
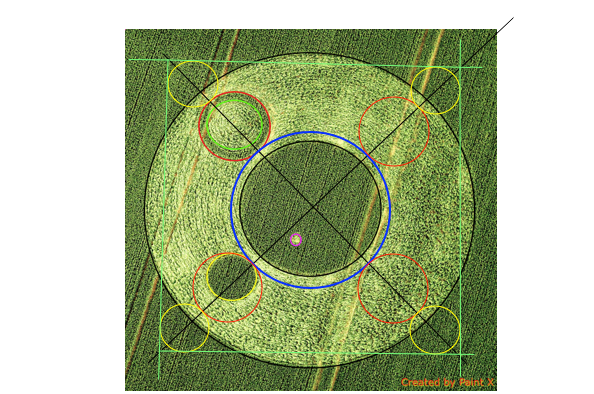
There are four tramlines cutting the crop circle.
Just now i notice that circle 7 (the inner perimeter of the circle with the standing ring; green in the image) touches the second tramline from the left.
The perimeter of the central circle (circle 2) touches the tramline on the most right.
Now i see: i found a second method of squaring circle 6!!
5) THE THIRD SQUARING
The steps are as follows:
-
Draw a line in the tramline on the utter right touching circle 2.
-
Draw a line tangent to circle 2 and circle 7: it appears to run parallel to the tramlines and so parallel to the line of step 1,
3) Connect the lines of step 1 and 2 by two lines with 90 degree angles, tangent to circle 2
4) Result: a square and a second method of squaring the -virtual- circle 6 (drawn in blue)
This square has, of course, the same size as the square of the first method.
The second method of squaring the circle maybe should be the FIRST ONE because it is defined by the tramlines in the field
and these were all that the circle makers had to work with.
Making crop circles which size and position are defined by tramlines happened before, see for instance the Barbury Castle formation on June 1st 2008.
6) AFTERWORD
Squaring the circle: okay, but squaring a virtual circle: great.
Finding two methods of squaring the circle: ever done before?
But then: all honour goes to the Circle Makers: what a fine way to show what you are able to and to let us discover it!
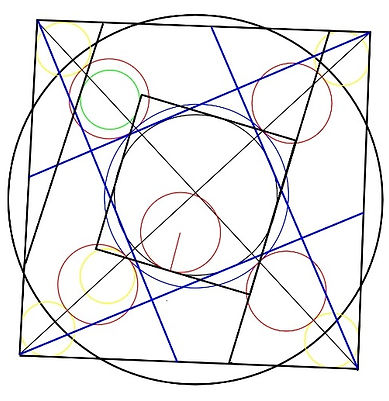
On left the the three ways of squaring the circle in one image. On the right overlayd with an octogram: a result of combining
the two ways of squaring the central circle of standing crop.